[FRM] 파이썬으로 VaR 구현하기 1

VaR은 포트폴리오 리스크 매니징에서 가장 기본적으로 사용되는 metric으로 최극단의 위험에서의 해당 포트폴리오가 잃을 수 있는 손실로 포트폴리오의 최대가능손실이라고 생각하면 된다. VaR은 크게 세가지 방법으로 구분되어지는데 1) 가장 쉬운 방법으로 포트폴리오 수익률은 나열하여 가장 큰 손실을 해당 포트폴리오의 VaR로 선정하는 것이고 2) 두번째 방법은 공분산행렬을 사용하는 것으로 과거의 수익률이 미래에도 유사할 것이라는 것과 포트폴리오의 손실이 정규분포를 따를 것이라는 전제하에 계산하는 방법으로 parametric-VaR이라고 하자 3) 마지막으로 몬테카를로 시뮬레이션을 사용하는 방법으로 과거 수익률을 random하게 sampling하여 수익률에 대한 분포를 만드는 것으로 nonparmametric-VaR이라고 한다.

​

첫번째 방법은 너무나도 원시적인 방법이기 때문에 스킵하고 두번째, 세번째 방법을 파이썬으로 구현해보자.

우선, parametric VaR방법이다.

​

Parametric-VaR을 구하는 방법은 다음과 같은 단계를 거친다.

포트폴리오의 각 자산별 수익률을 계산한다.

각 자산별 공분산행렬을 계산한다.

포트폴리오의 평균과 표준편차를 계산한다.

포트폴리오 수익률이 정규분포를 따른다는 가정하에 특정 confidence interva에서의 해당포트폴리오 역누적분포함수(분위수함수)를 계산한다.

포트폴리오 최초 투자금액(액면가)에서 4에서 계산한 quantile 값을 차분해 해당 포트폴리오의 최대가능 손실액을 계산한다.

​

다음으로 파이썬을 활용해 계산하는 방법을 알아보겠다.

​

우선, 관련 패키지를 import 하겠다. 포트폴리오 자산은 애플, 페이스북, 씨티그룹, 디즈니이고 데이터는 yahoo finance 패키지를 사용한다.

import pandas as pd
from pandas_datareader import data as pdr
import yfinance as yf
import numpy as np
import datetime as dt

tickers = ['AAPL','FB','C','DIS']
weights = np.array([0.25,0.3,0.15,0.3]) #포트폴리오 가중치

initial_investment = 1000000

data = pdr.get_data_yahoo(tickers, start = '2018-01-01', end = dt.date.today())['Close']

returns = data.pct_change()

returns.tail()

다음으로 공분산행렬(variance covariance matrix)를 만든다. 공분산행렬을 직접 만들수도 있지만, cov()라는 함수를 사용했다. 공분산행렬을 간단히 설명하면, 변수들간의 공분산(covariance)를 matrix notation으로 표현한 것으로, 아래와 같이 대각원소는 해당 변수들의 분산이고 대각원소를 제외한 나머지는 변수들간의 공분산을 symmetric하게 나타낸 matrix이다.

\[\begin{aligned} C(x,y,z)=\begin{pmatrix}\text{var}_x&covar_{x,y}&covar_{x,z}\\covar_{y,x}&var_y&covar_{y,z}\\covar_{z,x}&covar_{z,y}&var_z\end{pmatrix} \end{aligned}\]

#공분산행렬 만들기
cov_matrix = returns.cov()
cov_matrix

그리고 포트폴리오의 평균 수익률과 표준편차를 구하는데, 포트폴리오 평균 수익률은 각 자산의 평균 수익률과 가중치 곱으로 나타내는데 파이썬에서 프로그래밍하기 위해서는 각 자산의 평균 수익률과 가중치가 각각 벡터화 되어 있으므로 dot()함수로 내적해주면 포트폴리오 평균을 구할 수 있다.

\[AVG_{portfolio}=W_{APPL}\times AVG_{APPL}+W_{CL}\times AVG_C+W_{DIS}\times AVG_{DIS}+W_{FB}\times AVG_{FB}\]

또한 포트폴리오 표준편차는 앞서 구한 공분산행렬로 계산된다.

\[\sigma _{portfolio}^2=\sqrt{W"\cdot V_{portfolio}\cdot W}\] \[\left(AVG_x:x\text{의 평균 },W_x:x\text{의 가중치 },V_x:x\text{의 공분산행렬 },\sigma _x^2:x\text{의 분산 },\sigma _x:x\text{의 표준편차}\right)\]

마지막으로 초기 투자금액을 포트폴리오 평균과 포트폴리오 표준편차에 곱해준다.

#포트폴리오 평균 수익률 및 표준편차 계산
avg_rets = returns.mean()
port_mean = avg_rets.dot(weights) #포트폴리오 가중치 벡터와 내적해 수익률 normalization
port_stdev = np.sqrt(weights.T.dot(cov_matrix).dot(weights)) #포트폴리오 표준편차 계산
mean_investment = initial_investment*(1+port_mean) #포트폴리오 평균수익 계산
stdev_imvestment = initial_investment*port_stdev #포트폴리오 수익 표준편차 계산

위에서 구한 값들을 토대로 95%신뢰수준하에 분위수값을 계산하기 위해 수익률의 역누적분포함수를 scipy패키지로 구하게 되면 95%신뢰수준에서의 quantile 값 cutoff1 967906.7207564594원이 된다.

#역누적분포함수(ppf) 계산
from scipy.stats import norm
conf_level1 = 0.05
cutoff1 = norm.ppf(conf_level1, mean_investment, stdev_imvestment)
cutoff1

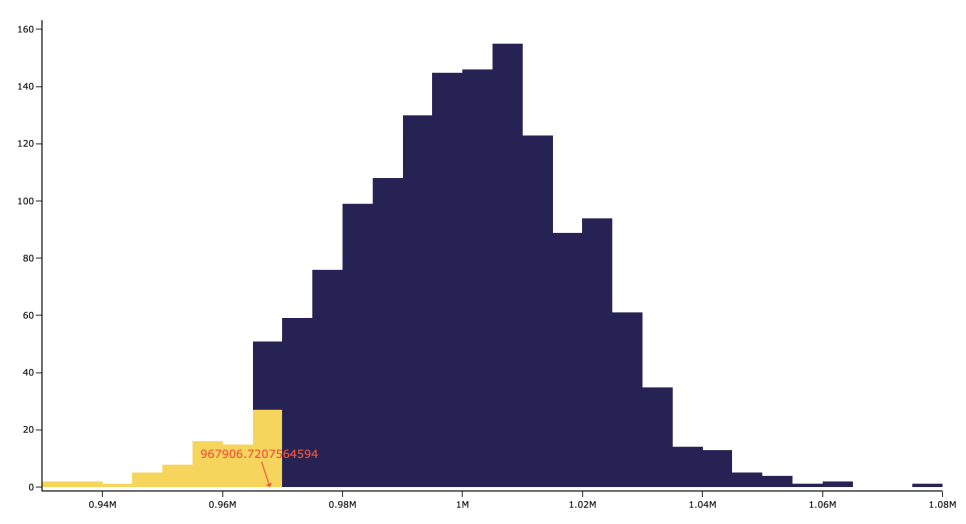
최종적으로 최초의 투자액 1,000,000원에서 극단값 cutoff1을 차분하면 95%신뢰수준에서 해당 포트폴리오의 최대가능손실액 약 22,347원을 계산할 수 있다.

​

참고: https://www.interviewqs.com/blog/value-at-risk