[Causal Inference] Asymmetric Causality Tests Applicaton

이 논문은 자산 변동간 granger causality를 실증분석한 논문으로 Abdulnasser Hatemi-J 교수가 2011년에 Empirical Economic에 기재한 논문이다. 해당 논문 이전에는 자산간 인과관계를 일반적인 변동성으로 검증하였는데 해당 논문에서는 자산의 변동성이 positive일때와 negative일때로 구분하여 asymmetric하게 자산간 인과관계를 검증하였다. 또한, 검증된 인과관계를 경제학 이론인 ‘Efficient Market Hypothesis’를 주장하는데 사용하였다.

1. Random Walk

모델링의 가장 근본이 되는 개념은 경제학, 통계학에서 time series를 다룰때 사용하는 random walk로부터 시작된다. 두 자산 \(y_1\) 과 \(y_2\) 에 대해 t시점의 자산의 가치는 \(t-1\) 시점의 자산 가치와 백색소음(white noise, error)로 표현된다. 허나 시점을 최초에서부터 생각하면 결국 t시점의 자산가치는 최초의 가치(initial value)로부터의 white noise의 누적 합과 동일하게 된다.

\[y_{1t}=y_{1t-1}+\epsilon _{1t}=y_{1,0}+\Sigma _{i=1}^t\epsilon _{1i}\]

\(y_{2t}=y_{2t-1}+\epsilon _{2t}=y_{2,0}+\Sigma _{i=1}^t\epsilon _{2i}\) 그리고 이때 white noise를 positive, negative일때로 구분해보면, positive일때는 특정시점의 error term이 최대일때 이고, negative일때는 특정시점의 error term이 최소일때이다. 즉, negative shock와 positive shock의 합으로 error term을 표현할 수 있다.

\[y_{1t}^+=\Sigma _{i=1}^t\epsilon _{1i}^+,\ \ \ y_{1t}^-=\Sigma _{i=1}^t\epsilon _{1i}^-,\ \ \ y_{2t}^+=\Sigma _{i=1}^t\epsilon _{2i}^+,\ \ \ y_{2t}^-=\Sigma _{i=1}^t\epsilon _{2i}^-\] \[y_{1t}=y_{1t-1}+\epsilon _{1t}=y_{1,0}+\Sigma _{i=1}^t\epsilon _{1i}^++\Sigma _{i=1}^t\epsilon _{1i}^-\] \[y_{2t}=y_{2t-1}+\epsilon _{2t}=y_{2,0}+\Sigma _{i=1}^t\epsilon _{2i}^++\Sigma _{i=1}^t\epsilon _{2i}^-\]

2. VAR(Vector Auto Regression)

위의 randomwalk의 개념이 특정 자산의 \(t\) 시점의 가치는 해당 자산의 \(t-1\) 시점에 영향을 받는 것이었다. 이를 확장해 Vector Auto Regression 모델은 자산 A,B에 대해 A,B가 서로 영향을 주고, 시점이 \(t-1\) 시점 뿐만 아니라 이틀전, 한달, 일년 등등 더 다양하게 고려할 수 있는데 이때의 시점을 lag라고 하고 보통 \(p\) 로 표현한다.

벡터로 이루어진 자산 y1, y2의 positive shock에 대해 VAR 모델은 다음과 같다.

\[y_t^+=v+A_1y_{t-1}^++\cdots +A_py_{t-p}^++u_t^+\]

\(y_t^+:\ 2\times 1\) vector of the variances
\(v:\ 2\times 1\) vector of intrcepts
\(u_t^+:\ 2\times 1\) vector of error terms
\(A_r:\ 2\times 2\) estimated variance-covariance matrix of error term
그렇다면, lag는 어떻게 선택해야 할까? lag의 경우 0부터 최대 lag p까지를 input 시켜 아래의 제약식이 최소로 되는 lag를 선택한다.

\(HJC=\ln (|\hat{\Omega }_j|)+j\left(\frac{n^2\ln T+2n^2\ln (\ln T)}{2T}\right),\ \ \ \ j=0,\cdots ,p\) \(\mid \hat{\Omega }_j \mid\) : covariance-variance matrix of error temrs

3. Hypothesis Test

마지막으로, wald statistic을 구하여 가설검증을 시행한다. 해당 논문에서의 귀무가설은 자산 A는 B에 non-granger cause하다 이다. 즉, 귀무가설을 reject하면 자산A는 B의 granger cause이고, 귀무가설이 채택되면 A는 B에 non-granger cause로 인과관계가 없다는 뜻이다.

\(H_0\): the row \(w\), column \(k\) element \(A_{r} = 0\) 그리고, 이때의 matrix notation은 다음과 같다.

\[Y=DZ+\delta\] \[\begin{align} & Y := (y_1^+, \cdots{}, y_T^+) \text{ } (n \times T) \text{ matrix} \\ & D := (v,A_1, \cdots{}, A_p) \text{ } (n \times (1+np)) \text{ matrix} \\ & Z_t := (1, y_t^+, \cdots ,y_{t-p+1}^+)' \text{ } ((1+np) \times 1) \text{ matrix, for }t= 1,\cdots{},T\\ & Z := (Z_0, \cdots{}, Z_{T-1}) \text{ } ((1+np)\times T) \text{ matrix}\\ & \delta:= (u_1^+, \cdots{}, u_T^+) \text{ } (n \times T) \text{ matrix} \end{align}\]

가설검증에 사용되는 통계량은 Wald Statistic(왈드 통계량)으로 귀무가설 값과 제한조건이 없는 추정치 사이의 거리를 기반해 파라미터의 제약을 평가할때 사용하는 통계량이다.

\[\text{Wald }=(C\beta )'[C((Z'Z)^{-1}\otimes S_U)C']^{-1}(C\beta )\]

\(S_U\) : covariance matrix of the unresricted VAR, \(\frac{\hat{S_U'}\hat{S_U}}{T-q}\) \(\beta =vec(D)\) \(\otimes\) : Kronec \(\ker\) product

마지막으로 해당 데이터를 bootstrap하여 bootstrap rotation마다의 Wald Statistic을 구한다. 그 이유는 finance data는 non-parametric하기 때문에, error term이 heteroskedastic하다. 그러므로 bootstrap으로 조건부하에 homoskedastic한 분포를 만들어 이분산성을 최소화 하기 위함이다.

그리고, bootstrap으로부터 계산된 wald statistic을 오름차순으로 ordering하여 quantile confidence interval critical value를 구하여 해당 값보다 bootstrap하지 않았을때의 값이 크게되면 귀무가설을 reject하게된다.

4. Empirical Process

가설검증에 사용된 데이터는 Oil Price, UAE Stock Price로 UAE경제에 큰 영향을 주는 oil price가 UAE stock에 non-granger causality인가를 검증에 사용하였다.

우선, 모델 자체에 대한 검증을 시행했다. 앞서 말했듯이 Finance data는 non-parametric하므로, VAR 모델들에 대한 multivariate normality를 검증했을때 모든 모델이 multivariate normality를 만족한다는 귀무가설을 reject하였고, ARCH effect를 고려한 bootstrap 모델의 VAR을 평가했을때는 모델은 non multivariate ARCH를 만족한다는 귀무가설을 세 가지 모델에 대해 rejcet하였고 두개 모델에선 valid하여 bootstrap에 대해서는 조건부 하에 모델이 homoskedastic하다라고 말할 수 있어, 해당 실험이 유의미하다고 판단할 수 있다. 또한 아래 표에서는 위의 제약식에서 구한 최적의 lag도 표기되어 있다.

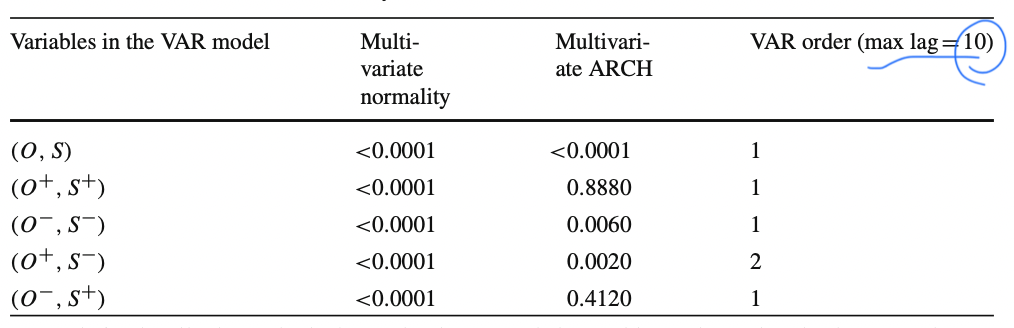
모델에 대한 검증을 시행했으니 다음으로 가설검증 결과를 비교해보았다.

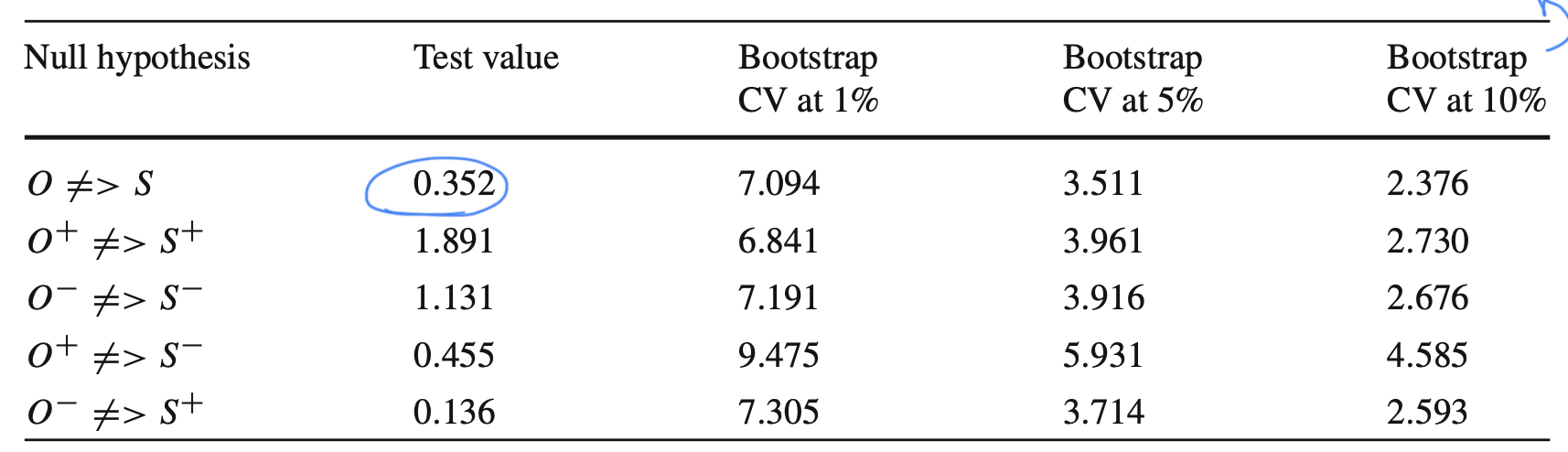
결론부터 말하면 모든 VAR모델에서 oil price는 UAE stock에 non-granger causality하다는 귀무가설을 reject 할 수 없었다. 즉, 국제 유가의 전일 변동성이 positive하던 negative UAE주가의 변동성에는 유의미하게 인과관계를 형성하지 못한다는 것이고, 효율적 시장 가설의 semi-strong form인 과거의 주가 데이터로 미래를 예측할 수 없다는 가설을 뒷받침하는 증거로 사용할 수 있게 되었다.

5. Causality Between KOSPI and S&P500

위에까지가 해당 논문의 내용이었고, 현시점을 기준으로 지난 10년동안의 데이터를 통해 S&P500이 KOSPI에 non-granger causality한지 알아보았다. 가설검증 프로세스는 논문과 동일하다.

데이터를 살펴보면 위와 같이 KOSPI, S&P500 모두 지난 10년동안 추세적으로 우상향 하며 두 index 사이에 어느정도 상관관계가 존재하다는것을 알 수 있었고, KOSPI의 경우 S&P500보다 변동성이 클 것으로 예상된다.

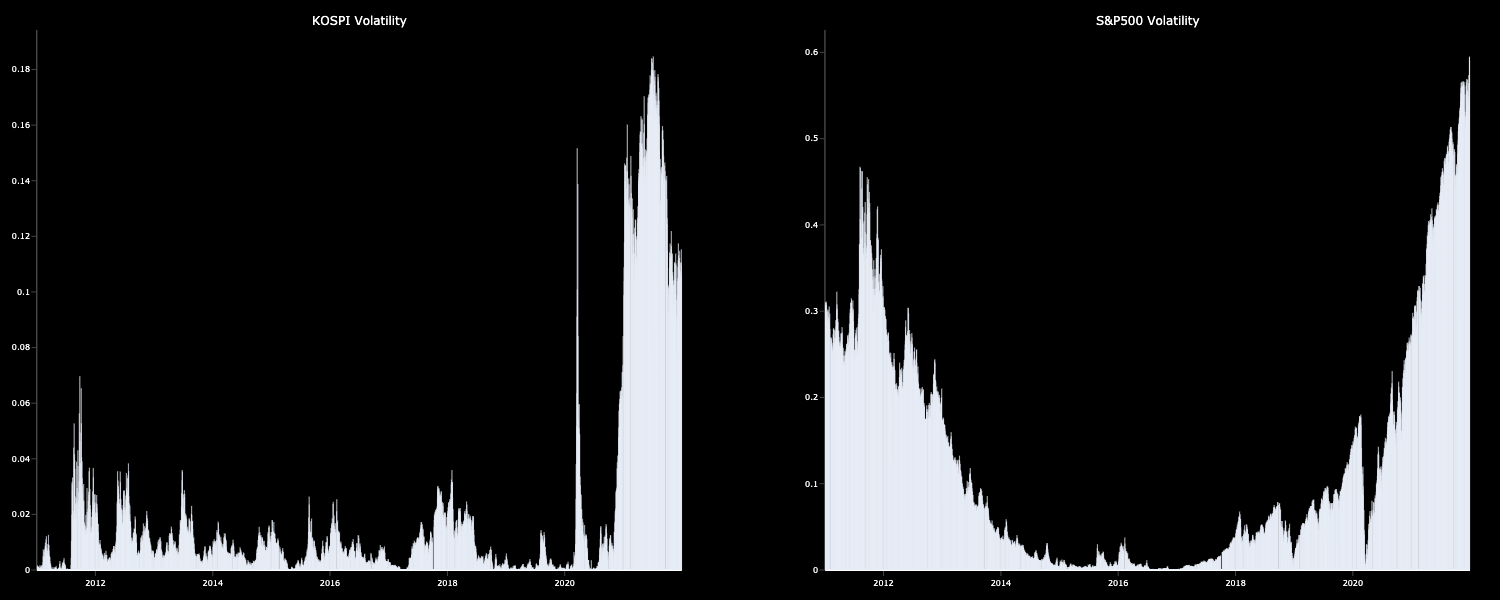
변동성 그래프를 보아도 지난 2020년 전까지 박스권에 머물렀던 KOSPI의 변동성은 최근보다 상당히 낮으며, 코로나19가 확산되었던 2020년 초반 변동성이 증가하더니 최근까지 변동성이 큰 것을 확인할 수 있었고, S&P500도 변동성이 일정하지 않음을 알 수 있다. 즉, ARCH 모형에 따라, 두 index의 volatility는 non-stable하며 heteroskedastic하기 때문에 현상태에서 모델링을 시행하면 유의미하지 않기 때문에 bootstrap이 필요함을 알 수 있다.

최종적으로 두 index 사이의 모든 confidence interval에서의 causality는 없는 것으로 검증되었다. 물론 미국 시장이 우리나라 시장에 영향을 주는건 맞지만, endogeneous한 또다른 변수가 존재할 것이고, direct로 두 index가 granger cause하다고 보기에는 제한점이 있다고 판단된다.